1. 
2. Help
3. Log In

Growth, Reproduction Rate

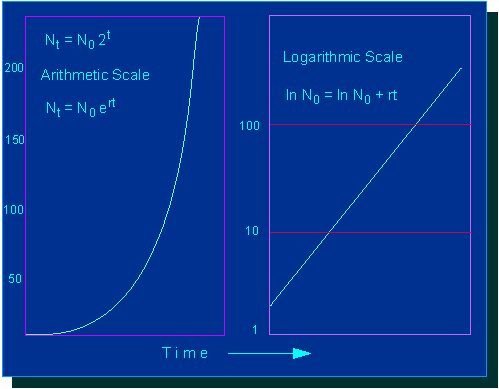
Growth kinetics in arithmetic and logarithmic representation

A population of N_t individuals is at the time t very large. During a finite period of time (t), the number of individuals changes due to new (b) and leaving individuals (d). This means that

delta N_t = (b - d) N_t t ,

with the difference between b and d being the rate of growth. The growth rate again depends on

the number of progeny / generations,

the number of generations per time,

and the chance of survival under the given environmental conditions.

More simplified, the equation runs:

delta N_t = rN_t t ,

If delta t > 0, then

delta N_t / dt = rN_t

The same equation written in its integrated state runs

rt = ln N_t - ln N₀ ,

with N₀ being the original number of individuals and N_t being the number of individuals at the end of the time period dt.

Remodelled, the equation runs

n_t= N₀ e ^rt or

ln N_t = ln N₀ + rt,

This latter equation is the formula of the general growth function though it is valid only under idealized conditions, i.e. during the logarithmic growth phase of a bacteria culture or a culture of single-celled algae.

e^r is the same as w that symbolizes the fitness (Wright’s fitness) of the individuals. If, for example, the fitness of an individual is 1 and that of another is 2, then the second individual produces twice the amount of progeny of individual 1. Resolved to r, the above formula runs

r = ln w

The growth rate is accordingly the same as the log naturalis of the value of the fitness, which again depends on the selection coefficient (s):

w = 1 - s