Triangulation Numbers
© 1994 Jean-Yves Sgro.
Institute for Molecular Virology/
jsgro@facstaff.wisc.edu
Introduction
This is a brief description with ASCII drawings of the notion of triangulation
numbers (T numbers) as used in virology. The basic principles were outlined by
Caspar and Klug (1962) extending mathematical knowledge to biological structures.
They also introduced the notion of quasi-equivallence for large virus structures
for which the large number of proteins could not explain strict icosahedral
symmetry.
Topology of Icosahedra
An icosahedron can be constructed by folding a plane with an order
of symmetry of 6: uniform hexagonal net.
/\ /\ /\ /\ /\ /\ /\ /\ /\ /\ /\ /\ /\ /\ /\ /\ /\ /\
\/__\/__\/__\/__\/__\/__\/__\/__\/__\/__\/__\/__\/__\/__\/__\/__\/__\/__\
\ /\ /\ /\ /\ /\ /\ /\ /\ /\ /\ /\ /\ /\ /\ /\ /\ /\ /
__\/__\/__\/__\/__\/__\/__\/__\/__\/__\/__\/__\/__\/__\/__\/__\/__\/__\/
/\ /\ /\ /\ /\ /\ /\ /\ /\ /\ /\ /\ /\ /\ /\ /\ /\ /\
_/__\/__\/__\/__\/__\/__\/__\/__\/__\/__\/__\/__\/__\/__\/__\/__\/__\/__\
\ /\ /\ /\ /\ /\ /\ /\ /\ /\ /\ /\ /\ /\ /\ /\ /\ /\
__\/__\/__\/__\/__\/__\/__\/__\/__\/__\/__\/__\/__\/__\/__\/__\/__\/__\
/\ /\ /\ /\ /\ /\ /\ /\ /\ /\ /\ /\ /\ /\ /\ /\ /\ /
\/__\/__\/__\/__\/__\/__\/__\/__\/__\/__\/__\/__\/__\/__\/__\/__\/__\/
\ /\ /\ /\ /\ /\ /\ /\ /\ /\ /\ /\ /\ /\ /\ /\ /\ /\
__\/__\/__\/__\/__\/__\/__\/__\/__\/__\/__\/__\/__\/__\/__\/__\/__\/__\
/\ /\ /\ /\ /\ /\ /\ /\ /\ /\ /\ /\ /\ /\ /\ /\ /\ /\
\/__\/__\/__\/__\/__\/__\/__\/__\/__\/__\/__\/__\/__\/__\/__\/__\/__\/__\
Each hexagon can be decomposed into 6 equilateral triangles. One hexagon
is flat. If you remove one of the triangles you need to be in 3 dimensions
to connect the 2 free edges, constructing a pentamer.
________remove one
hexamer is flat. | triangle.
________ V
/\ /\ /\ /\
/ \ / \ / \ / \
/ \ / \ / \ / \
/______\/______\ /______\/______\
\ /\ / \ /\ /
\ / \ / \ / \ /
\ / \ / \ / \ /
\/______\/ \/______\/
If the hexagon is not isolated but part of a gigantic net, the net will
now have a curvature and be in 3 dimensions. If this folding is repeated
12 times on 12 contiguous hexagons an regular icosadeltahedron is obtained
(T=1,see below). Each of the 12 vertices is at the center of a pentagone.
If the hexagones had been chosen further apart from each other, i.e. non-adjacent,
it is clear that the closed structure formed would be bigger! This new structure
is not a homothetic transformation of the icosadeltahedron because it now
contains pentagones AND hexagones. Pentagones are still located at the 12 5-fold
vertices whatever size the new structure assumes.
Triangulation Number
The uniform hexagonal net helped to visualize the formation of icosahedral
structures by transforming some hexagones into pentagones. Pentagones and
hexagones can both be considered to be constructed by the same building
block represented by the equilateral triangular units. 2 sides of this
'unit triangles' represent 2 unit vectors generating the net. Hence they
can be used to describe the coordinates of the points of the various hexagones
and pentagones.
The vector between 2 neighbouring 5-fold vertex can be expressed as a function
of those 2 unit vectors. Each of the 12 vertices are equivallent and choosing
any one of them will define all possibilities of triangulations. The triangulation
number is defined as the square of the distance between 2 adjacents 5-fold vertices.
___________________
/\ /\
/ \ / \
/ \ / \ Let O be a 5-fold vertex and
/ \ / \ OH and OK the 2 axes on the unit
/ \ / \ equilateral triangle generated by
/ - M - \ the unit vectors of the net.
/ OK _ / | \ _ \ The 2 unit vectors form a 60
/ _ / | \ _ \ degree angle.
/ _ / | \ _ \ Let M be a neighbouring
/O - | - _\ 5-fold vertex with coordinates (H,K).
\ - _ | _ - / The vector OM can be decomposed
\ \ _ | - / / as the sum of the vectors OH and OK.
\ \ _ | - / /
\ OH \ _ | _ / / The triangulation number can then be calculated:
\ ^ /
\ / \ /
\ / \ / 2 2 2
\ / \ / T = OM = OH + OK + 2 OH.OKcos60
\ / \ /
\/_________________\/ since cos60 = 0.5:
2 2
T = H + HK + K
If f is the largest common divisor between H and K:
2 2 2 2
T = f ( h + hk + k ) = f P
P is called the class of the icosahedron and can assume a *limited* number of
values (1,3,7 etc.). H and K can be any integer (including zero) and h and k
are integers without any common factor.
The icosahedron has 20 triangular faces. Any icosahedron will have 20T faces,
12 pentamers and 10(T-1) hexamers.
The triangulation number can be graphically determined with the following
drawing arranged from Caspar and Klug (1963).
_
/\ \ D
/__\ \ E
/\ /\ \ X
/__\/__\ \ T
/\ /\ /\ \ R
/__\/__\/__\ \ O
/\ /\ /\ /\ \ ,P=3
/__\/__\/__\/__\ \ ,'
/\ /\ /\ /\ /\ _\ ,'
/__\/__\/__\/__\/__\ , '
/\ /\ /\ /\ /\ /, ' _
K: 5_/__\/__\/__\/__\/__\75_\91 \ L
/\ /\ /\ /\ /\, /\ /\ \ A
4_/__\/__\/__\/__\48_\61_\76_\93 \ E
/\ /\ /\ /\, /\ /\ /\ /\ \ V
3_/__\/__\/__\27_\37_\49_\63_\79_\97 \ O
/\ /\ /\' /\ /\ /\ /\ /\ /\ \
2_/__\/__\12_\19_\28_\39_\52_\67_\84_\ \
/\ /\' /\ /\ /\ /\ /\ /\ /\ /\ \
1_/__\3__\7__\13_\21_\31_\43_\57_\73_\91_\ \
/\' /\ /\ /\ /\ /\ /\ /\ /\ /\ / \
/__\/__\/__\/__\/__\/__\/__\/__\/__\/__\/ _\
T: 1 4 9 16 25 36 49 64 81 100
| | | | | | | | | |
H: 0 1 2 3 4 5 6 7 8 9 10
FIGURE LEGEND: Triangulation numbers T=(H2+HK+K2) represented on an equilateral
triangular net. An icosahedron with a 5-fold vertex at the origin of this net
and a neighbouring 5-fold vertex at the lattice point of index H,K will have
10T+2 vertices (12 five- and 10[T-1] six-connected vertices) and 20T triangular facets.
Point O corresponds to a 5-fold vertex and the first neighbouring 5-fold vertex,at point
M has coodinates (H,K). Point M is uniquely defined as a function of T if T is *on* either
axis OH or Ok (i.e. if K=0 *or* H=0) or if T has a value on the bissectrice. In the first
two cases the icosahedron class is P=1, for the latter case the class is P=3.
For any other number there is a left/right asymmetry. In these cases for a given
triangulation number there exists 2 possibilities for the position of point M
and the corresponding icosahedra are mirror images of one another. In the above
drawing only the P=1,P=3 and laevo numbers are positioned.
For instance to arrive on the T=7 on the laevo side one would start at point O
and advance 2 unit length on the H axis and then one would "turn left" to jump
one length on the K axis. The number 7 is located there on the figure. If one would
have started with the K axis one would obtain the symmetrical point on the other
side of the bissectrice which would be 7 d. (Klug and FInch, 1965).
Quasi-equivalence: T number and P number
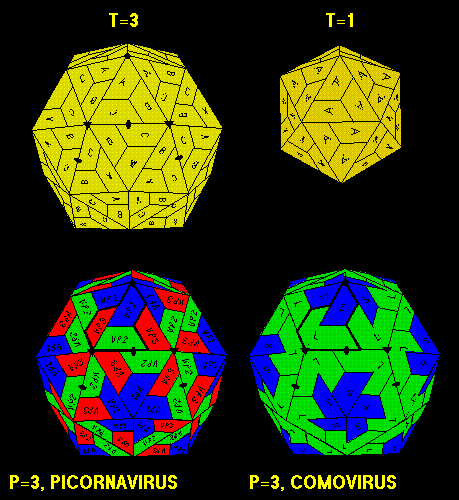
The icosahedron has 2,3 and 5-fold symmetry. Each of the 20 facets of a T=1 icosahedron
have a real icosahedral 3-fold symmetry. Hence each triangle can be subdivied into
3 equal portions. If each portion contains one coat protein, for a total of 20x3=60 proteins,
each protein is in exactly the same environment as any other. Coat proteins are
all chemically identical (have the same sequence).
If the icosahedron has a higher Triangulation number, even if all proteins are
chemically identical, some will be in an environment of 5 neighbors (5-fold vertex
area: pentagones) and others will be in a 6 neighbors environment (hexagones). Hence
the postioning of each protein is not equivallent between each protein and any other
but only quasi-equivallent.
Most T=3 viruses have 180 proteins (3 proteins x 60 triangles). Their positions is
often refered to as A, B and C quasi-equivallent positions. All A proteins are
equivallent to one another, and similarly for B and C proteins.
A | A
5 Within each of the 60
. '/ \` . triangles fits about 1 each of
, / \ ` . A,B and C. The symmetry axes are
, A / \ A ` . \ labeled 5,2,3. q3 is a *quasi*
, / A \ ` ` . \ 3-fold axis within the triangle.
, / \ ` ` .\ Around the icosahedral
/ / \ ` B ' 5-fold are five As.
C / / \ `. . ./ But around the 3-fold
/ / \ / are 3 B and 3 Cs
B /_______q3/ \ / / alternating.
/ \ \ /
\ / \ B \ C /
/ C \ \
\ / \ \ / B A proteins form pentagones, B and C form
C__3/___________2_____\_________\3 __ hexagones.
\ |
B \ \ / \ C
C \ B \ C / \
\ \ / B \
\ \_________/
\ / /
/
A
If the proteins are not chemically identical (as in poliovirus, rhinovirus etc.)
the quasi-equivallence is refered to as pseudo-equivalence. The quasi 3-fold axis
is called a pseudo 3-fold axis. The triangulation number of rhinovirus is mathematically
T=1. However the structure of the virion closely resembles that of a T=3 virus. Hence
these viruses are refered to as having a p=3 meaning they have a pseudo-T=3 number.
Note that p=3 is written with a small p and should not be confused with P=3 the class
of icosahedra with T=3 symmetry!
VP1 | VP1
5 Within each of the 60
. '/ \` . triangles fits about 1 each of
, / \ ` . VP1-3. The symmetry axes are
, VP1 / \ VP1 ` . \ labeled 5,2,3. p3 is a pseudo
, / VP1 \ ` ` . \ 3-fold axis within the triangle.
, / \ ` ` .\ Around the icosahedral
/ / \ ` VP3 ' 5-fold are five VP1s.
/ / \ `. . ./ But around the 3-fold
/ / \ / are 3 VP2s and 3 VP3s
VP3 /_______p3/ \ / / alternating.
/ \ \ / In Plant viruses with T=3
\ / \ VP3 \ VP2 / symmetry the similarity is
/ VP2 \ \ with VP1=A, VP2=C, VP3=B.
\ / \ \ / VP3
VP2__3/___________2_____\_________\3 __
\ |
\ \ / \ VP2
VP2 \ VP3 \ VP2 / \
\ \ / VP3 \
\ \_________/
\ / /
/
References
Caspar D.L.D. and Klug A.,(1962). Physical principles in the construction of regular
viruses. Cold Spring Garbor Symp. Quant. Biol. 27,1-24.
Caspar D.L.D. and Klug A., (1963) Structure and assembly of regular virus particles.
Virus, nucleic acids and cancer. Williams and Wilkins, Baltimore, Maryland, USA, 2-39.
 Go to the
top page
Go to the
top page
Content: ©1994-1997 Stephan Spencer &
Jean-Yves Sgro
Design: ©1997
Internet Concepts, LLC
Web Design by