Das Mikroskop ist das wohl am häufigsten genutzte Hilfsmittel vieler Biologen. Der Grund hierfür liegt auf der Hand: Zellen sind die Grundeinheiten allen Lebens, und ihre Größe liegt, von wenigen Ausnahmen abgesehen, unterhalb der Auflösungsgrenze des menschlichen Auges. Es gibt zahlreiche Angaben darüber, daß die Brechung des Lichts an Glaslinsen oder mit Wasser gefüllten Kugeln sowie das sich hieraus ergebende Vergrößerungsvermögen bereits im Altertum bekannt waren. Im 13. Jahrhundert hat der britische Philosoph und Naturforscher Roger BACON Segmente von Glaskugeln als Vergrößerungsgläser (Lupen) verwendet und sie sehbehinderten Personen als Brille empfohlen. Auch das Schleifen von Linsen entwickelte sich in den folgenden Jahrhunderten zu einer immer vollkommeneren Fertigkeit.
Nach einer Überlieferung des Arztes P. BORCH sollen Hans und Zacharias JANSEN (Vater und Sohn) aus dem holländischen Middelburg Anfang des 17. Jahrhunderts durch Hintereinanderschaltung zweier Linsen das zusammengesetzte Mikroskop erfunden haben. Gleichzeitig werden sie auch als Erfinder des Fernrohrs genannt. Nach anderen Quellen wird C. J. DREBBEL (1572-1634) aus Alkmaar als Erfinder des Mikroskops angesehen. Selbst wenn das nicht zutreffen sollte, hat er sich um die Verbreitung von Mikroskopen verdient gemacht. Die Bezeichnung Mikroskop wurde von Mitgliedern der römischen Accademia de Lincei (Akademie der Luchsäugigen) eingeführt, deren prominentestes Mitglied G. GALILEI war.
Unabhängig von der anlaufenden Entwicklung der zweilinsigen (zusammengesetzten) Mikroskope wurde der Einsatz immer stärker vergrößernder Linsen ("einlinsige Mikroskope") vorangetrieben. Wieder war es ein Holländer, A. van LEEUWENHOEK, dem es gelang, Linsen mit etwa 270facher Vergrößerung (Brennweite 1 mm) zu konstruieren und erfolgreich mit ihnen zu arbeiten (siehe Abbildung: links aus: W.A.W.MOLL: Antonius Leeuwenhoekius Delphis Natus MDCXXXI). Mit seinen Untersuchungen hatte der Einsatz "einlinsiger Mikroskope" seinen Höhepunkt erreicht.
Wie schon berichtet, erschien 1667 die "Micrographia" des britischen Naturforscher Robert HOOKE, der mit Hilfe eines zweilinsigen Mikroskops pflanzliche Gewebe untersuchte und ihren Aufbau aus Zellen erkannte. Die Fortentwicklung und vor allem der Einsatz von Mikroskopen im 18. Jahrhundert verlief nur zögernd. Das beruhte zum einen auf der Ansicht namhafter Naturforscher, das Mikroskop sei entbehrlich, weil es noch vieles zu entdecken gäbe, wozu man es nicht benötige, und zum anderen auf störenden Farbfehlern (chromatische Aberration). Letztere waren die Ursache für zahlreiche Fehlinterpretationen, die zu dem Vorurteil führten, mit dem Mikroskop könne man alles sehen, was man sehen wolle.
Zur Minderung diese Handicaps hatte D. GREGORY bereits 1695 erwogen, Farbfehler durch Kombination von Linsen unterschiedlicher Dispersion zu reduzieren. 1771 gab der Mathematiker L. EULER eine theoretische Begründung für Achromate (farbkorrigierte Linsensysteme) und schlug vor, solche achromatischen Objektive zu berechnen. Gebaut wurden sie schließlich von F. G. BEELDSNYDER (1735-1808), der zwischen zwei bikonvexe Linsen aus Kronglas (mit einem bestimmten Brechungsindex) eine bikonkave Linse aus Flintglas (mit einem vom Kronglas verschiedenen Brechungsindex) einschloß.
Fortentwickelt wurden achromatische Linsensysteme durch G. D. AMICI (1786-1863), auf den auch die Erfindung von Immersionsobjektiven zurückgeht.
Der eigentliche Durchbruch auf dem Weg zur Konstruktion moderner Mikroskope erfolgte nach der Ausarbeitung der Theorie der Bildentstehung im Mikroskop durch E. ABBÉ (1840-1905). Er bewies, daß eine absolute, von der Objektivapertur und der Lichtwellenlänge abhängige Leistungsgrenze der mikroskopischen Abbildung existiert. Seine Theorie erlaubte es, hochleistungsfähige Mikroskope reproduzierbar und somit serienmäßig herzustellen.
Der Einsatz neuentwickelter Glassorten durch O. SCHOTT (1851-1935) führte 1886 zur Entwicklung apochromatischer Objektive (hierbei wird ein als "sekundares Spektrum" bezeichneter Farbrest beseitigt) durch E. ABBÉ und C. ZEISS. Durch die Fortschritte im Mikroskopbau ermöglicht, folgten in der zweiten Hälfte des vorigen Jahrhunderts in rascher Folge zahlreiche Entdeckungen auf den Gebieten der Histologie, Cytologie und Bakteriologie. Gefördert wurde der Trend durch die Entwicklung und den Einsatz geeigneter Fixierungs-, Einbettungs- und Schneideverfahren (Mikrotom), spezifischer Farbstoffe und von Konservierungsmitteln.
Je
näher man einen Gegenstand an das Auge heranführt, desto mehr
Einzelheiten sieht man, wobei aber sehr schnell die Grenze erreicht wird,
bei deren Unterschreiten das Auge den Gegenstand nicht mehr scharf abbilden
kann, da der Krümmungsradius der Augenlinse nur in bestimmten Grenzen
variierbar ist. Beim menschlichen Auge liegt diese Grenze, auch Bezugssehweite
genannt, bei 250 mm (Durchschnittswert erwachsener Menschen). Das Auge
sieht den Gegenstand unter dem Sehwinkel G. Beim Betrachten eines Gegenstands
interessiert, wie genau Einzelheiten erkannt werden können. Mit anderen
Worten: ob zwei benachbarte Punkte gerade noch als getrennt wahrgenomrnen
werden können. Das Maß für die Unterscheidbarkeit zweier
Punkte ist das Auflösungsvermögen. Zum Beobachten von Objekten,
die unter der Auflösungsgrenze des Auges liegen, benötigt man
ein Vergrößerungsglas (eine Lupe), deren Vergrößerung
sich nach der Formel
V = 250 [mm] / f [ mm]
berechnet.
Hierbei sind die 250 mm die Bezugssehweite des menschlichen Auges und f die Brennweite der Linse. Kennt man die Vergrößerung einer Lupe und möchte die Brennweite errechnen, formuliert man die Beziehung um und erhält
f [mm] = 250 [mm] / V
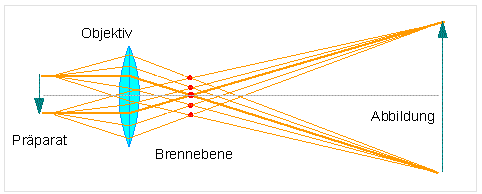
Möchte man Objekte noch stärker vergrößern, benötigt man zwei hintereinandergeschaltete Linsen(systeme) [Objektiv und Okular] und ist damit bereits beim Mikroskop. Durch das Objektiv wird das Objekt (O) vergrößert, es entsteht ein reelles, umgekehrtes Zwischenbild (O'). Dieses wird durch das Okular nachvergrößert. Man erhält O'', welches man als umgekehrtes Bild im Abstand von ca. 250 mm erkennen kann. Die Vergrößerung eines Mikroskops ist damit das Produkt von
VObjektiv und VOkular
Strahlengang im Mikroskop:
F = Brennebene, O = Objekt,
Ob = Objektiv,
Ok = Okular
Das Auflösungsvermögen ist jedoch ausschließlich durch das Objektiv bedingt. Zur Beschreibung eines Objektivs genügt nicht nur der Vergrößerungsfaktor, sondern als weitere Größe wird die numerische Apertur (A) benötigt. Darunter versteht man
A = n sin alpha
wobei n der Brechungsindex des Mediums zwischen Objekt (bzw. dem Deckglas) und der Frontlinse des Objektivs ist. In der Regel ist dieses Medium Luft mit dem Brechungsindex n = 1. a ist der Öffnungswinkel, unter dem ein Strahl vom Objektiv gerade noch aufgenommen werden kann; dieser Winkel (alpha) kann niemals größer als 90 Grad sein, und somit kann auch die numerische Apertur (unter der Bedingung n = 1) niemals Werte über 1 annehmen. In der Praxis bildet der Wert 0,95 die oberste Grenze, weil der Abstand zwischen Objektiv und Deckglasoberfläche nicht den Wert 0 annehmen kann. Die Apertur von 0,95 entspricht einem Öffnungswinkel alpha von ca. 72 Grad. Eine Steigerung des Aperturwerts ist durch die Wahl eines anstelle der Luft stärker brechenden Mediums zwischen Objektiv und Deckglasoberfläche erreichbar. Hierzu hat sich das Immersionsöl mit einem Brechungsindex von n = 1,515 bewährt. Es ist wenig sinnvoll, noch stärker brechende Verbindungen einzusetzen, denn dann wäre der Brechungsindex des Deckglases und der Linsen der limitierende Faktor (n = 1,525). Immersionsöl läßt sich nur bei speziell konstruierten Immersionsobjektiven verwenden. Bei einem maximalen Öffnungswinkel von 67,5 Grad erhält man dann eine Apertur von 1,515 x 0,92 = 1,40. Ist die Apertur eines Objektivs bekannt, kann man nach der Formel
d = lambda / 2 A (Ojektiv)
das Auflösungsvermögen und somit die maximale (förderliche) Vergrößerung bestimmen. Wie ersichtlich, spielt lambda, die Wellenlänge des Lichts, eine entscheidende Rolle. Ist lambda = 550 nm (= grünes Licht), ergibt sich folgende Beziehung zwischen Auflösungsvermögen und Apertur:
d = 550 [nm] / 2 x 1,40 = 200 nm = 0,2 µm
0,2 µm (Mikrometer = 1/1000 Millimeter) ist folglich die theoretisch höchste Auflösung, die mit einem Lichtmikroskop erreicht werden kann.
In grober Annäherung kann gezeigt werden, daß das Auflösungsvermögen des Lichtmikroskops bei Verwendung eines starken Immersionsobjektivs etwa bei der halben Lichtwellenlänge liegt. Kennt man die Auflösungsgrenze eines Mikroskops, läßt sich die maximale (förderliche) Gesamtvergrößerung ermitteln.
Eine Vergrößerung gilt dann als förderlich, wenn die gerade aufgelösten Punkte (im Abstand von 0,2 µm) so stark vergrößert werden, daß sie vom Auge als klar getrennte Einheiten zu sehen sind. Bei einer Bezugssehweite von 250 mm beträgt die Auflösung des menschlichen Auges ca. 0,15-0,2 mm. Als Faustregel wird daher angegeben, daß die förderliche Vergrößerung bei etwa
500-1000 x A (Objektiv)
liegen sollte, bei einem Objektiv mit der Apertur 1,4 also bei maximal 1400fach.
Licht hat bekanntlich Wellencharakter, und es ist deshalb nötig, sich mit einigen grundlegenden Prinzipien der Wellenoptik auseinanderzusetzen, um eine Bildentstehung im Mikroskop deuten zu können, vor allem aber, um die Grundlagen moderner lichtmikroskopischer Verfahren wie Phasenkontrast-, Polarisations- und Interferenzkontrastmikroskopie zu verstehen. Zunächst daher einige Begriffe und deren Definitionen:
Amplitude, Frequenz, Wellenlänge und Phase und Interferenz sind die wichtigsten Parameter, um einen Wellenzug zu beschreiben.
Die Wellenlänge des sichtbaren Lichts liegt zwischen 400 und 800 nm. Die Interferenz ist die gegenseitige Beeinflussung zweier Wellenzüge, wobei die Wellenberge verstärkt oder abgeschwächt werden können (Amplitudenverstärkung, Amplitudenreduktion). Im Extremfall können zwei Wellen einander auslöschen.
Unter Beugung versteht man die partielle Ablenkung (eines Lichtstrahls) an den Kanten lichtundurchlässiger Objekte. Zur Veranschaulichung ist es sinnvoll, sich Beugungserscheinungen an einfachen, spalt- oder lochförmigen Blenden klarzumachen. Stellt man hinter eine solche Blende einen Schirm in den Strahlengang, kann man das Beugungsbild abbilden. Es besteht aus sich zum Rand hin abschwächenden regelmäßigen Folgen von Punkten oder Linien.
Die Musterzusammensetzung und -anordnung hängt von der Art der Blende oder des verwendeten Objekts (z.B. einem mikroskopischen Präparat) ab. Doch stets sind die Muster um eine zentrale Achse (hier: unvergrößertes Projektionsbild der Blende) angeordnet.
Verwendet man eine Blende mit zwei Öffnungen, wird das Licht an den Rändern beider gebeugt. Die Beugungsbilder der nunmehr zwei Strahlen überlagern sich und man erkennt daher in regelmäßigen Abständen Verstärkungen und Abschwächungen
Um ein vergrößertes Bild zu erhalten, müssen die ersten Nebenmaxima des Beugungsbildes mit erfaßt werden (E. ABBÉ). Die Abstände der Punkte im Beugungsbild sind umgekehrt proportional zu den entsprechenden Abständen im Objekt. Zur Rückverwandlung eines Beugungsbildes in ein reales Bild, bedarf es einer Sammellinse (im Mikroskop: Objektiv), deren Apertur groß genug ist, die Intensitätsmaxima (-I, +I) einzufangen. Das "Zwischenbild" kommt durch das Zusammenwirken von gebeugtem und nicht gebeugtem Licht zustande.
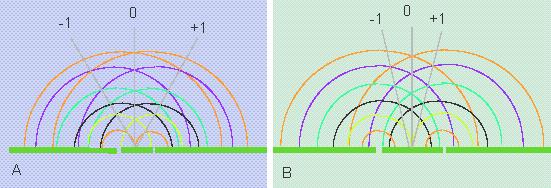
Beugungserscheinungen an Spalten. Je näher zwei Spalten (oder Lochblenden), an denen eine Beugung des Lichts stattfindet, beeinanderliegen, desto größer ist der Winkel, unter dem die ersten Intensitätsmaxima der Beugung erscheinen; um so größer muß folglich auch die Apertur einer Linse sein, um sie noch einfangen zu können.
Vergrößerungen, so wie hier beschrieben, lassen sich auch durch andersartige Strahlung erzeugen. Die für Biologen wohl wichtigste Ergänzung des Lichtmikroskops ist das Elektronenmikroskop, bei dem die Ablenkung (Beugung an Atomkernen) eines Elektronenstrahls nutzbar gemacht wird. Ferner ist die kurzwellige Röntgenstrahlung zu nennen, die sich zur Aufklärung von Molekülstrukturen eignet (M. v. LAUE, L. BRAGG, Ergebnisse). Da es aber keine Sammellinsen für Röntgenstrahlen gibt, muß die im Beugungsbild enthaltene Information mathematisch verrechnet werden, um die Struktur des Moleküls zu ermitteln.
|
