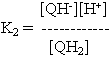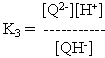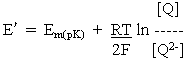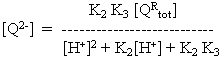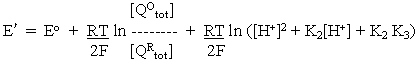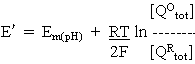Lecture 7Protons as ligands
|
Proton as a ligand
In a previous lecture we considered how the redox potential of a half-cell in which a proton was a reactant was modified by pH. The proton acts as a weak ligand, and the treatment previously given was appropriate only over pH ranges away from the pK value(s) for the proton dissociation(s). In order to treat the full pH range, and systems in which more than one proton dissociation occurs, we treat the proton as the ligand and apply the above treatment.
We will consider the quinone/hydroquinone (quinone/quinol) system as an example.
QH2 --> Q + 2H+ + 2e-
The oxidized form, Q, shows no proton dissociations, but for the quinol form, we have several possible dissociations, as previously discussed:
QH2 <==> QH- + H+ ----- pK2
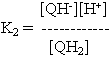
QH- <==> Q2- + H+ ----- pK3
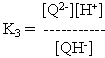
In addition to the half-cell reaction for the neutral quinol shown above, the two anionic quinols have their own half-cell reactions:
QH2 ==> Q + 2H+ + 2e- (below pK2) (z=2, n=2)
QH- ==> Q + H+ + 2e- (above pK2) (z=2, n=1)
Q2- ==> Q + 2e- (above pK3) (z=2, n=0)
We will consider the system in terms of the total activities of oxidized and reduced forms:
[QOtot] = [Q]
[QRtot] = [QH2] + [QH-] + [Q2-]
For reaction at pH >> pK2 or pK3, where all the quinol is present in the Q2- form,
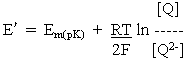
where Em(pK) is the Em value above the highest pK, where the value is independent of pH.
At any other pH, the concentrations of the different forms can be found by substitution in the equations above. For example,
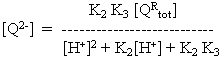
Rearranging and substituting between the two equations above, we find that
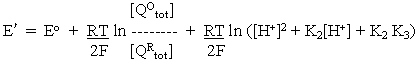
where
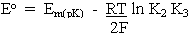
At any particular value of pH, the term is parentheses is constant, giving us the familiar equation derived in the previous lectures:
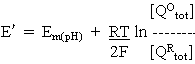
where
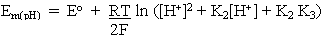
©Copyright 1996,
Antony Crofts, University of Illinois at Urbana-Champaign,
a-crofts@uiuc.edu