LON-CAPA GENETIC DIVERSITY

Best estimates of biodiversity value:
using genealogy to predict genetic or character richness

Principles
Phylogenetic & taxonomic measures
Lack of phylogenetic information

Principles
Biologists needing to estimate richness in a particularly valued currency of different genes or characters are usually unable to measure this directly, or at best are only able to study small samples of genes or characters. However, because genes and characters are inherited, biologists have been able to respond by proposing phylogenetic or taxonomic measures of diversity. These measures predict the biodiversity value of different biotas, using knowledge of the genealogical (or hierarchical) relationships among organisms in combination with models of gene or character evolution (ref 2, ref 3).

To illustrate how classifications may be used to predict diversity value by estimating richness at the level of the genes or characters, the example below shows a classification for some African species of milkweed butterflies (family Nymphalidae). The branching pattern of the classification is derived by analysis of 217 morphological and chemical characters, and the branch lengths are scaled by the number of character changes found within this sample (shown as vertical ticks). Considering all combinations of three species, the most diverse set of three species is niavius, echeria and damocles, because these three have the longest total branch lengths with the largest numbers of character differences between them (shown in black) (below):

To illustrate how using this approach can effect the relative values of different faunas or floras, consider first one of the most popular measures of diversity, species richness. The example below shows counts of the numbers of species of sibiricus-group bumble bees among equal-area grid cells (below):

Link to image showing results of species richness measure.

For these bumble bees, a large representative sample of character-difference data is not yet available, only a genealogical classification. Nonetheless, a simple evolutionary model can still be used to estimate the way changes in characters for these bees are likely to have accumulated, given this classification tree. When combined with a measure of tree length to count the relative expected number of character differences within each fauna, the next example shows an improved prediction of relative diversity value for the same bee faunas, to take into account the expected numbers of gene or character differences (below):

Link to image showing results of phylogenetic diversity measure.

Phylogenetic & taxonomic measures
In the absence of complete knowledge of the valued genetic or character differences among organisms, the most direct approach to estimating relative value is to use phylogenetic measures. This is used to scale the branch lengths on the tree for use by the measure in the third step. It can use sample data for gene or character variation, or it can be based on just a taxonomic classification, if that is all that is available and if it is believed to represent genealogical relationships. These require three components (ref 2):

1. Cladograms
The phylogenetic approach is based on the general evolutionary model of descent with modification: that genes and characters are inherited, with rare alterations or changes. Some of these changes are reversals, so that data often conflict with any one tree (homoplasy), although such conflicts are minimised in the construction of cladograms. If the resulting trees are good estimates of genealogical relationships, then they should be more reliably predictive of the unsampled genetic or character variation, which always remains the great majority.

2. Models of gene/character evolution
Next, an explicit choice has to be made of a special evolutionary model for linking the branching pattern of the tree with the way genes or characters change along the tree (ref 2). Three extreme options for this model are envisaged (below):

The �*clock*� (anagenetic) model assumes that changes occur at random and are subject to little constraint by selection. Consequently, in effect, changes accumulate more or less in proportion to the time elapsed along the branches.		Result: if sample data are unavailable or are expected to be biased and unrepresentative, all lineages are scaled to a common length.

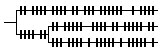The *sample* (empirical) model assumes that the distribution of changes in a small sample of variation is representative of the great majority of unsampled variation. The pattern of changes is usually expected to be intermediate between those from the other two models.		Result: if sample data are available and are expected to be representative, all branches are scaled in proportion to sample changes.

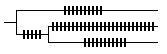The *saltatory* (cladogenetic) model assumes that most changes are associated with speciation or divergence events, for example if strong selection constraints are relaxed at these times. Although the numbers of changes associated with each branching event may differ, in effect changes accumulate more or less in proportion to the number of branching events (including those to extinct branches).		Result: if sample data are unavailable or are expected to be biased and unrepresentative, all branches are scaled to unit length.

3. Measure of gene/character richness
Third, a measure of relative richness in different genes or characters is needed, which sums the relative degree of change along the tree using the branch lengths scaled by the chosen special evolutionary model. There is now broad agreement on the form of this measure, as a measure of the length of the subtree that spans any given set of species of interest on the tree. A simple case of this measure is illustrated graphically, for calculating the increase in diversity (or complementary diversity) when a species C is added to a tree for two species A and B from the pairwise differences between species, AB AC and CB (below):

For the example of the butterfly cladogram shown at the top of the page, branch lengths can be scaled on the horizontal axis (the vertical components should be ignored) using the three evolutionary models described above. For each model, the set of three species that is estimated to have the greatest genetic or character richness is sought. For this tree, only with the sample model is there a unique solution. With the other models, there are at least two equivalent choices for each species, as shown by the vertical tie bars (below):

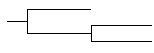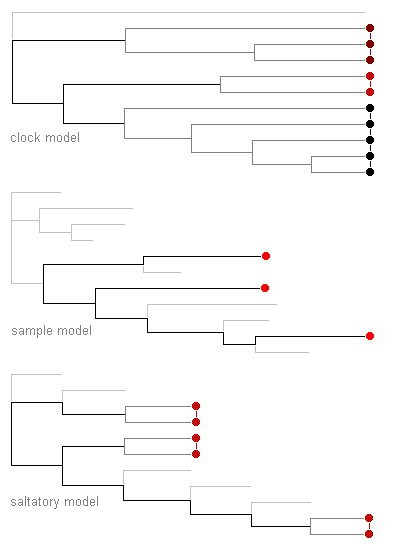
Most disagreement is now centred on the choice of special evolutionary model (ref 2). The sample model is the easiest to use, and its consequences in this example show that it may given less equivocal answers concerning which species represent the greatest relative diversity.

However, the apparent advantages of the sample model are only real if the sample truly represents the overall pattern of variation. For example, if a sample of unconstrained genetic data were available that behaved as though following the clock model, whereas the value being sought for expressed characters was under strong stabilising selection and distributed as though it followed the saltatory model, then using the sample model could introduce a severe bias into the measure. Consequently, any apparent increase in resolution arising from using information from the sample in this way could actually be misleading.

Lack of phylogenetic information
In practice, detailed and reliable phylogenetic (genealogical and difference) information is often unavailable. Nevertheless, arguments for measuring biodiversity value as gene or character richness do at least provide a philosophically and economically defensible starting point, as one possible answer to the problem of what is valued in diversity. Accepting that phylogenetic or taxonomic diversity measures can use genealogical pattern as a predictor of value also provides a possible key to the problem of finding more practical measures (ref 4).

Copyright (c) 1998 The Natural History Museum. Please read the disclaimer.